Capacitor Materials Crystallization Nucleation Study

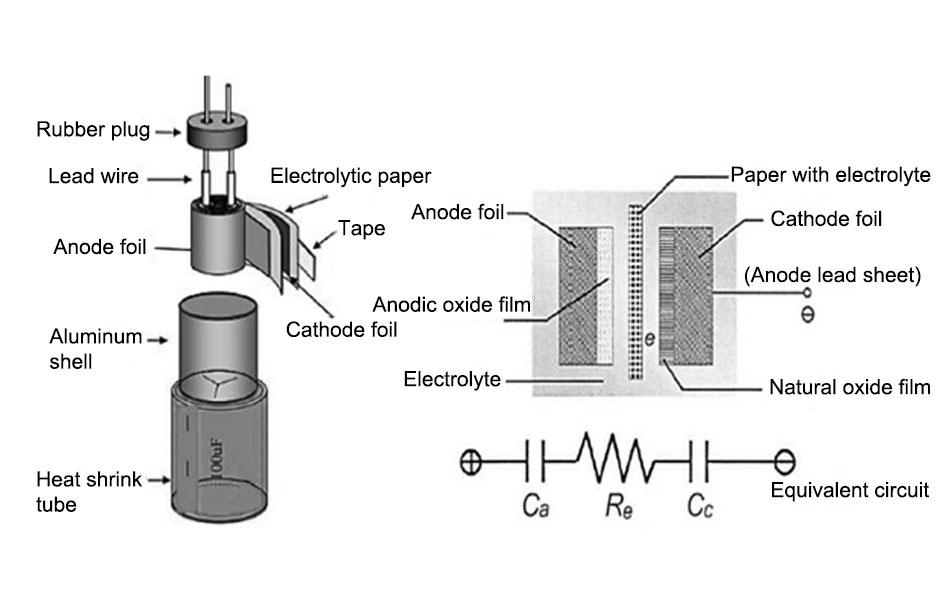
In casting and rolling production, the requirements for melt modification are very strict, especially for direct casting and rolling of electrolytic aluminum liquid. A slight negligence may cause malignant defects and lead to product scrapping. For example, in the casting and rolling process of capacitor materials, slight composition fluctuations may affect the final performance. In order to understand this problem, the physical and chemical changes that occur during the crystallization process are first introduced here.

The crystallization of the melt must go through the process of nucleation ⟶ growth ⟶ crystallization completion, among which nucleation is very important. The number of cores formed is large, the growth rate of the crystal nucleus is slow, and the grain size is fine.

When the melt crystallization is not modified, it is a process of spontaneous nucleation and crystal nucleus growth. The aluminum melt at the crystallization front is a metastable fluid in a metastable state. The process of nucleation and growth of the metastable fluid is a process of free energy change in the body. The reduction of Gibbs free energy caused by the transformation of a single atom or molecule in a metastable fluid into an atom or molecule in a stable phase (crystal) is Δg. Assuming that the atomic volume or molecular volume in the crystal is Ω_s and the interface energy between the crystal and the fluid is r_sf, the free energy change caused by the formation of a spherical crystal with a radius of r in a metastable fluid is:

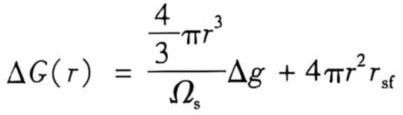(1)

For a spherical crystal with a radius of r, which is a collection of i atoms or molecules, then:

(2)

(3)

where η – shape factor.

For a cube, the shape factor is:&nbsp

(4)

For a sphere, the shape factor is:

(5)

Considering geometric bodies of different shapes, their shape factors η are different. At the same time, η is related to the atomic volume Ω_s. Substituting equation (3) into equation (2), we get:

(6)

Equations (1) and (6) respectively show the change in free energy caused by the formation of a spherical crystal with a radius of r and the appearance of a spherical crystal composed of i atoms or molecules in the fluid phase, that is, the energy required to form the above-mentioned crystal nucleus. ΔG is also called formation energy, which is the sum of two terms. The first term iΔg, if the fluid is a metastable phase, the body free energy Δg is negative, that is, iΔg is negative, otherwise it is positive. The second term is the change in interfacial energy caused by the appearance of a body in the fluid, also known as surface free energy, which is always positive.

When Δg>0, that is, it is a stable fluid, the system appears crystal, and its free energy is increased. This phenomenon cannot occur automatically. For aluminum melt, the capacitor materials, there is no supercooling, so it is impossible for nuclei and crystallization to occur.

When Δg<0, the volume free energy term is negative, which decreases with the increase of i and r, and decreases with r³. The surface free energy term is positive and increases with the increase of r². It can be seen that when r>r*, or i>i*, ΔG decreases with the increase of r, and the body in the metastable fluid will automatically grow (see Figure 1).

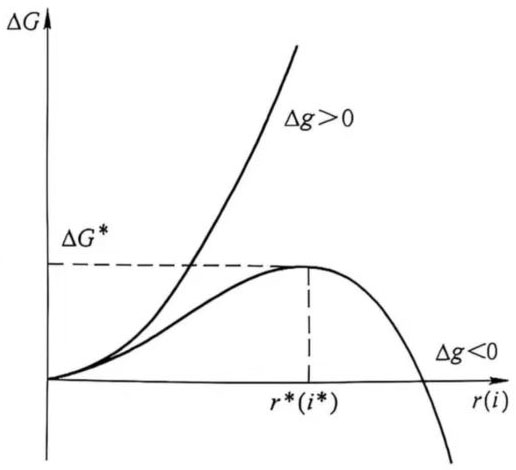
Figure 1 Relationship between the change of free energy of nucleation and size

Find the extreme value of ΔG(r) or ΔG(i) and set it equal to 0, that is, the critical radius r* and the critical number of atoms i* are obtained. From equation (1) and equation (6), we can get:

(7)

(8)

Substituting equation (5) into spherical crystals, we can get:

(9)

Substituting equation (7) and equation (8) of grain radius r* and atomic number i* into equation (1) and equation (6), we can get the formation energy of crystal nucleus:

(10)

(11)

Where L-latent heat of phase change per unit atom;

T_m-solidification point of melt;

ΔT-supercooling.

ΔG* is the energy fluctuation required for nucleation in metastable fluid. Without this energy fluctuation, the crystal nucleus cannot be formed.

When the energy fluctuations satisfy the formation energy of the crystal nucleus, the crystal nucleus can be generated. However, the number of crystal nuclei that can be generated per unit volume is related to the distribution law of the embryo clusters of the complex phase fluctuations in the fluid. In the study of capacitor materials, if the number of uncombined molecules or atoms per unit volume in the system is n, the number of embryo clusters per unit volume is:
(12)

(13)

Wherein, ΔG(r) and ΔG(i) are the formation energies of the embryo clusters with radius r and number of atoms i, respectively, expressed as:

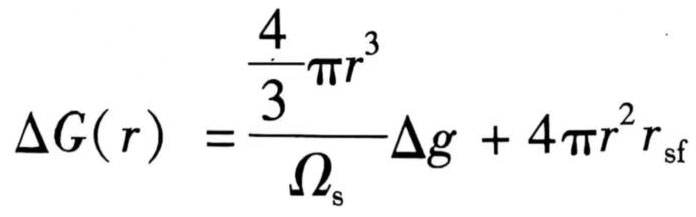(14)

(15)

For metastable fluids, the embryo clusters with Δg<0 and r<r* cannot grow, but the embryo clusters with r=r* can grow, and once they grow, they form macroscopic crystals. What we are concerned about here is the number of crystal nuclei per unit volume in the system, that is, the number of embryo clusters with r=r* is:

(16)

(17)

The nucleation rate of the crystal is not only proportional to the number of nuclei per unit volume, but also proportional to the probability of the nuclei capturing atoms or molecules in the fluid. Therefore, the crystal nucleation rate can be expressed as:

(18)

The probability of a crystal nucleus capturing an atom in a melt growth system is:

(19)

Where n-the number of uncombined molecules (or atoms) per unit volume in the melt;

ν0-the vibration frequency of atoms in the melt;

Δq–the diffusion activation energy of atoms across the solid-liquid interface.

Substituting equations (19) and (10) into equation (18), we get the nucleation rate of the melt growth system:

(20)

Equation (20) reflects the law of uniform nucleation in a metastable fluid without external cores. Generally speaking, under such conditions, it should present an equiaxed crystal structure after crystallization. However, the cooling rate of casting and rolling is very high, and the time from the melt flowing out of the casting nozzle to the completion of crystallization is about 1s. In such a short time, it is very unlikely that the process of nucleation and growth will go through energy fluctuations and complex phase fluctuations. In the manufacturing process of capacitor materials, the greatest possibility is that the melt flows out of the casting nozzle, contacts the water-cooled casting roller sleeve, and forms a spherical crown core on the roller sleeve substrate. Suppose the spherical cap crystal embryo is s, the radius of curvature of the spherical cap is r, and the contact angle at the junction of the three phases is θ (see Figure 2). Let the cosine of the contact angle be m, and assume that each interface energy is isotropic, then:

(21)

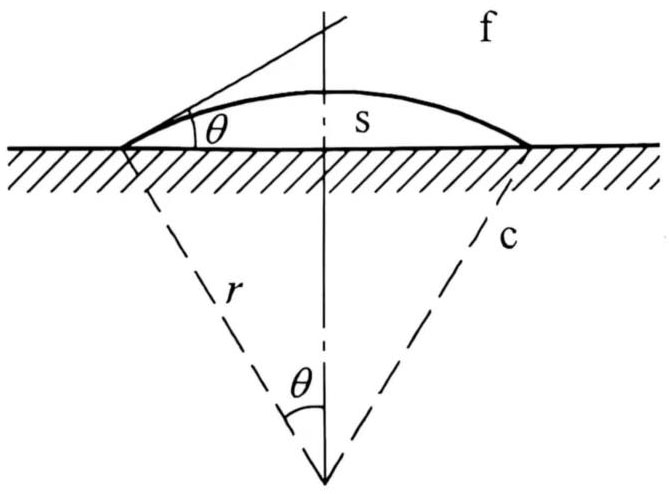
Figure 2 Formation of spherical cap nucleus on substrate

The embryo volume V_s, the interface area A_sf. between the embryo and the fluid, and the interface area A_sc between the embryo and the substrate can be calculated, respectively:

(22)

(23)

(24)

After the spherical cap nucleus is formed, the free energy change caused in the system is:

(25)

Substituting equations (22) to (24) into equation (25), using equation (21) Simplify, and we get:

(26)

Differentiate (26) with respect to r, and let , and we get the radius of curvature of the spherical crown embryo:

(27)

Substitute (27) into (26), and we get the formation energy of the spherical crown nucleus:

(28)

(29)

From equations (28), (29), and (10), it can be seen that the energy expression required to form a spherical crown nucleus on the roller sleeve substrate is different from the energy expression required for uniform nucleation in the melt, and the two differ by a factor ƒ₁(m). Now let’s discuss the properties of the ƒ₁(m) function to understand the difference and connection between uniform nucleation in the melt and non-uniform nucleation on a flat substrate. First, analyze the range of ƒ₁(m). The range of contact angle θ is 0°<θ≤180°, so the cosine of the contact angle m changes in the interval 1≥m>-1, so the range of ƒ₁(m) is 0≤ƒ₁(m)≤1. It can be seen that the substrate has the property of reducing the nucleation energy ΔG*, that is, nucleation on the substrate is much easier than uniform nucleation. In the study of capacitor materials, what is the difference and connection between nucleation on a flat substrate and uniform nucleation? From equations (29) and (21), it can be seen that the size of ƒ₁(m) is completely determined by the size of the interface energy between the substrate, the fluid and the crystal, or in other words, it is determined by the contact angle θ between the three phases. It can be seen that when θ=0°, ƒ₁(m)=0, the nucleus formation energy ΔG* on the substrate is 0, which indicates that nucleation is not required and the embryo can be immediately transformed into a crystal on the substrate. This is easy to understand physically, because θ=0°, indicating that the embryo (crystal) completely infiltrates the substrate, and a thin layer of body (embryo) with a macroscopic thickness will be covered on the crystallizer substrate, which is equivalent to seed crystal growth. When θ=180°, ƒ₁(m)=1, the formation energy of non-uniform nucleation on the substrate is completely equal to the formation energy of uniform nucleation, and the substrate does not contribute to the nucleation process. This is because θ=180° is a completely non-infiltrated situation. At this time, the embryo and the substrate are only tangent at one point, and the spherical crown embryo completely becomes a spherical embryo, so there is no difference from uniform nucleation. Therefore, in the melt growth system, substrates with different contact angles play different roles in the nucleation process.

The casting roll sleeve and casting crystallizer are neither completely nor incompletely wetted by the aluminum melt. It can reduce the nucleation energy, but it is impossible to grow directly on the substrate without forming a nucleus. Therefore, as soon as the melt contacts the roll sleeve, a spherical nucleus is formed on the substrate and quickly grows into a coarse grain structure (see Figure 3). In some applications, such as the production process of capacitor materials, the interaction between the crystallization characteristics of the material and the substrate will also affect the performance of the final product. Therefore, studying the influence of the substrate on the nucleation behavior is of great significance for optimizing the casting process and improving the microstructure of capacitor materials.