1. Vacancy
Capacitors – other defects in aluminum Vacancies in aluminum crystals are defects caused by missing atoms in normal positions in the structure. Vacancies can cause local distortions in the crystal structure, which are limited to a few atomic distances. Relative to the scale of the entire crystal, the spatial range involved in vacancies is very small, so they can be regarded as geometric points in the crystal structure, that is, zero-dimensional defects. Figure 1.35 shows a schematic diagram of vacancies in aluminum crystals and vacancies on the metal surface observed under a scanning tunneling microscope.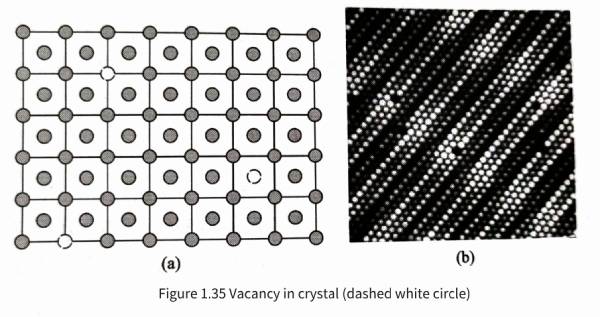
Vacancy is a point defect inherent in many aluminum crystals, which can have a certain equilibrium concentration. Vacancies can exchange positions with atoms, causing thermally activated transport of atoms. From a thermodynamic point of view, the existence or appearance of vacancies will cause an increase in thermodynamic enthalpy and a change in entropy in the crystal structure system. The concentration x of point defects in the crystal structure is generally low, that is, x<< 1. When the point defect concentration x changes by δx, the change in Gibbs free energy δG caused is
Where ΔHf is the enthalpy of vacancy formation, k is the Boltzmann constant, T is the thermodynamic temperature, klnx is the ideal mixing entropy, and Δsf can be approximately regarded as the vibration entropy caused by vacancy formation. At equilibrium, there are:
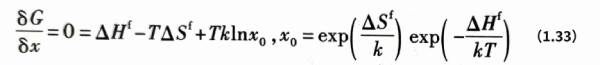
Where Xo is the equilibrium concentration of vacancies.
If only the interaction of the nearest neighbor atoms is considered, then for aluminum crystals with a coordination number of 12, Δsf=1.73k can be obtained with the help of a certain theoretical model. The vacancy formation enthalpy ΔHf of aluminum is about 1.217 52×10--19, the vacancy diffusion activation energy is about 1.041 3×10-19J, and the diffusion activation energy of aluminum atoms by vacancy self-diffusion is about 2.242 8×10-19J. The equilibrium concentration of vacancies in aluminum crystals is usually very low; when close to the melting point, the equilibrium concentration of vacancies can reach up to 2×10-3.
Aluminum materials are always at a certain processing or service temperature, so as shown in formula (1.33), a certain vacancy concentration will always be maintained in the material structure. Referring to the structure diagram given in Figure 1.35 (a), it can be imagined that when the atoms in a normal crystal jump out of their original equilibrium position under the action of thermal activation, a vacancy defect will be left at the original position. Usually, this jumping atom will enter the surface of the crystal or at the boundary between polycrystalline grains.
According to formula (1.33), temperature is an important factor affecting the vacancy concentration. Suppose that the macroscopic volume V of the crystal is expressed as L3, L is the one-dimensional size of the crystal, then its volume change during the heating process ΔV=Δ(L3)=3L2‘ΔL, and the volume change rate caused by macroscopic expansion can be obtained, ΔV/V=3ΔL/L. Similarly, it can be deduced that the volume change rate ΔV/V caused by thermal expansion of the crystal microscopic unit cell constant a is 3Δa/a. The macroscopic ΔL/L of the sample includes the volume change caused by the microscopic Δa/a change and the volume change caused by the change in vacancy concentration. From this, the vacancy concentration xVO can be calculated:
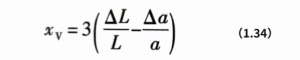
The thermal expansion rate ΔL/L of the macroscopic length L of the crystal can be measured by a dilatometer, and the thermal expansion rate Δa/a of the crystal unit cell constant a can be measured by a high-temperature X-ray diffractometer; thus, the relationship between vacancy concentration and temperature can be analyzed with the help of formula (1.34). Figure 1.36 shows the experimental values reflecting the variation of the macroscopic length and microscopic unit cell constant of the aluminum sample with temperature. It can be seen that with the increase of temperature, the expansion rate of the macroscopic length gradually exceeds the expansion rate of the microscopic crystal unit cell constant, that is, the vacancy concentration increases with the increase of temperature. According to the measured thermal expansion coefficient data at a series of temperatures, and with the help of the vacancy concentration calculated by formula (1.34), the formation enthalpy ΔHf and vibration entropy ΔSf of the crystal vacancy can be deduced by referring to formula (1.33), and then the general relationship between vacancy and temperature is obtained. Figure 1.37 shows the experimental observation of vacancy concentration at different temperatures, and the calculation using formula (1.33) (dashed line in Figure 1.37, ΔSf=1.73k, where k is the Boltzmann constant, ΔHf =1.217 52×10-19J); the two are generally consistent.
On the other hand, under the condition of external force, the external force may be converted into a normal stress perpendicular to the direction of the excess half-atomic plane of the edge dislocation. The interaction between this positive stress and the positive stress of the edge dislocation stress field [Formula (1.17)] will cause the edge dislocation to lose stability. When the positive stress converted by the external force exceeds a certain critical value, the edge dislocation may move in a direction perpendicular to the slip plane, which is called climb. Under the action of positive stress, the climb movement of the edge dislocation will cause the expansion or contraction of its excess half-atomic plane, so only the edge dislocation can climb. The edge dislocation line is actually the edge line of the excess half-atomic plane in the crystal, and it will move with the expansion or contraction of the half-atomic plane.
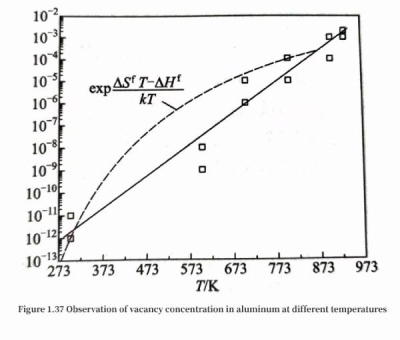Figure 1.38 is a schematic diagram of the climb motion of edge dislocation lines. There are many vacancies in the crystal before climb [Figure 1.38(a)], and the symbol x represents the vacancy position. Under the action of compressive stress perpendicular to the edge dislocation half-atomic plane, the edge of the edge dislocation line will relax the compressive stress by releasing atoms to occupy vacancies in the crystal, thus causing the contraction of the half-atomic plane, that is, the edge dislocation undergoes contraction climb [Figure 1.38(b)]. On the contrary, under the action of tensile stress perpendicular to the edge dislocation half-atomic plane, the edge of the edge dislocation line will adsorb normal atoms and simultaneously create new vacant atoms in the crystal [Figure 1.38(c)] to relax the tensile stress; thus causing the expansion of the half-atomic plane, that is, the edge dislocation undergoes expansion climb [Figure 1.38(c)]
Capacitors – Other defects in aluminum Figure 1.38
During the climb of edge dislocations, a whole row of atoms at the edge of the half-atomic plane cannot be adsorbed or released at the same time. The climb process is actually the process of atoms at the edge of the half-atomic plane detaching or joining one by one. Therefore, unlike the slip motion of dislocations, the climb of edge dislocations needs to be realized with the long-range migration of vacancies in the crystal, so the climb motion is more difficult than slip and is a relatively slow process. Usually, the climb of edge dislocations is not only driven by normal stress, but also requires the help of thermal activation process at higher temperatures. Dislocation climb will change the change of vacancy concentration in the crystal (see Figure 1.37), thereby causing a change in the crystal volume. The contraction climb of the half-atomic plane will cause the crystal volume to decrease, while the expansion climb of the half-atomic plane will cause the crystal volume to expand.
Capacitors – Other defects in aluminum The above is an explanation of vacancies.
2. Capacitors – other defects in aluminum-Structure of grain boundaries
Aluminum foil of electrolytic capacitors is a polycrystal composed of many small crystals of very small size (Figure 1.7). The size and geometric shape of each grain in a polycrystal are often different. There is a grain interface between grains in a polycrystal, referred to as a grain boundary. The arrangement of atoms near the grain boundary deviates from the arrangement of the internal structure of the grain, and is therefore in a state of irregular arrangement. Figure 1.39 schematically shows the state of grains with the same structure but different orientations aggregated together in a polycrystal. The essential difference between grains in aluminum polycrystals lies in their orientation differences, and this difference will also affect the structure and characteristics of the grain boundaries between grains. Grain boundaries have an important influence on the corrosion performance of aluminum foil.
The properties of grain boundaries depend on the structure of the grain boundaries, including the orientation difference of the grains on both sides of the grain boundary. The orientation difference of adjacent grains usually refers to the minimum rotation angle θ when the grains on one side of the grain boundary rotate around a specific [uvw] crystallographic direction to have the same orientation as the grains on the other side of the grain boundary. It is expressed as <uvw>θ. The actual structure of the grain boundary also includes the curvature of the grain boundary, the step structure of the grain boundary, local grain boundary defects, the distribution of heterogeneous atoms or precipitated phases on the grain boundary, etc.; therefore, the structure of the grain boundary is very complex. The grain boundary only involves the thickness of a few atomic layers. According to the orientation difference of the grains on both sides of the grain boundary, the grain boundary can be divided into small-angle grain boundaries and large-angle grain boundaries. The orientation difference is less than 10°, which belongs to the small-angle grain boundary, and the orientation difference is greater than 15°, which belongs to the large-angle grain boundary. Grain boundaries with orientation errors in the range of 10°~15° can be considered as small-angle grain boundaries or large-angle grain boundaries depending on the nature of the problem involved.
Capacitors – Other defects in aluminum Figure 1.39
Small-angle grain boundaries are composed of arranged dislocations and can be described by a simple model. If a crystal is first cut into two parts along a certain crystal plane, and then rotated around a certain direction on the cut surface by a very small angle θ, and then the cut surfaces of the two parts of the crystal are cut into parallel surfaces and merged together, the merged surface is a tilted grain boundary. Figure 1.40 (a) is a schematic diagram of a symmetrical tilted grain boundary in a crystal. The relative orientation of the two sides of the grain boundary is generated by rotating the angle θ, and the interface is a symmetry plane close to the low-index crystal plane. The joining of two grains in this way will inevitably produce distortion in the connection area, and these distortions can be relaxed on the interface by a row of edge dislocations with a Burgers vector length of b. It can be easily seen from Figure 1.40 (a) that the relationship between the dislocation Burgers vector length b, the dislocation spacing D and the rotation angle θ should be as follows: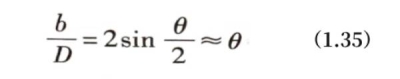
If the crystal interface is far away from the low-index crystal plane, an asymmetric tilted grain boundary can be formed. As shown in Figure 1.40 (b), the interface relies on two groups of edge dislocations with different Burgers vectors to jointly relax the distortion of the bonding surface. The Burgers vector of one group of dislocations is [100] (b⟂), and the Burgers vector of the other group of dislocations is [010] (b⊦), which are evenly distributed on the grain boundary. According to the geometric relationship of the grain boundary, the average spacing D⟂ and D⊦ of the ⟂ type dislocation and the ⊦ type dislocation can be calculated. If a crystal is first cut into two parts along a certain crystal plane, then rotated around the normal direction of the cut plane by a very small angle θ, and then the two parts of the crystal are merged together, the merged surface is a twisted grain boundary. Figure 1.40 (c) is a schematic diagram describing a twisted grain boundary. After the cut surfaces are merged, a large number of atoms on the merged surfaces are mismatched. If two sets of non-parallel screw dislocations are introduced to relieve these mismatches, the area of atomic position mismatch on both sides of the grain boundary will be significantly reduced [Figure 1.40 (c)], thereby reducing the energy of the grain boundary. The torsion grain boundary structure can be composed of two sets of non-parallel screw dislocations, and the distance between the dislocations is still D = b/θ.
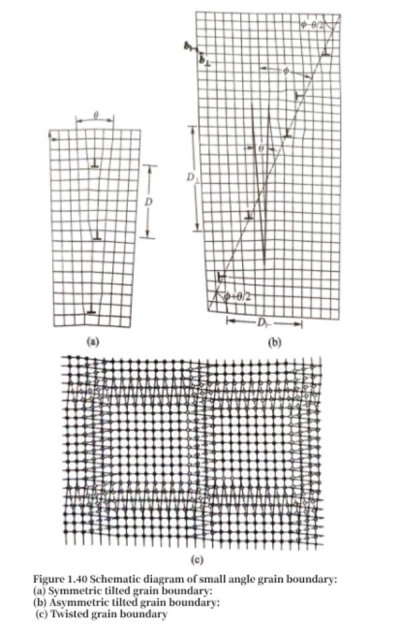The geometry of screw dislocations in general twist grain boundaries is network-like. Most actual small-angle interfaces are not pure tilt or pure twist grain boundaries, but a mixture of the two. When the misorientation angle of a grain boundary is greater than 15°, it becomes a large-angle grain boundary, and its structure is difficult to construct with dislocations. The irregular arrangement of atoms on the grain boundary will also cause an increase in energy.
Since the small-angle grain boundary structure is composed of a dislocation network, its grain boundary energy is the energy composed of these dislocations. Equation (1.35) shows that the grain boundary dislocation spacing is closely related to the misorientation angle, so the grain boundary energy is a function of the misorientation angle. For example, a symmetrical tilted grain boundary is composed of a set of parallel edge dislocation walls with a spacing of D = b/θ. The elastic stress field at a distance greater than D from the dislocation is basically offset, so the grain boundary energy depends on the stress field of the edge dislocation and the dislocation spacing D. Referring to equation (1.18), the energy of a dislocation per unit length on the grain boundary is EE. It can be rewritten as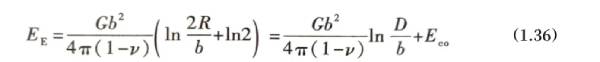
Where: EcoO can be regarded as the energy of the dislocation core that is not listed separately in equation (1.18); D is the spacing of dislocations on the grain boundary, D = 2R. The number of dislocations per unit area is θ/b. Substituting it into equation (1.36), the interface energy per unit area Ygb is
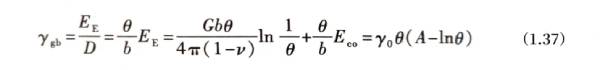
Where
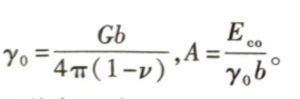
From formula (1.37), it can be seen that from θ=0, the grain boundary energy ygbincreases with the increase of θ. When θ is very large, the dislocations on the grain boundary are too close and interfere with each other. The simple dislocation energy can no longer explain the interface energy. Therefore, formula (1.37) is only applicable to small angle
(≤10°) grain boundaries. Substituting the parameters of pure aluminum G=25.9×109 N/m2b=0.2863×10-9m and v=0.36 into formula (1.37), and referring to formula (1.36), the relationship between the small-angle grain boundary energy of pure aluminum and the orientation difference angle θ can be obtained, as shown in Figure 1.41.
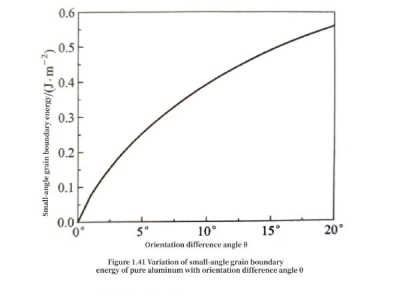
Capacitors – Other defects in aluminum Figure 1.41
The grain boundary energy is composed of the elastic energy of the long-range strain field of the grain boundary and the core energy of the atomic interaction in the narrow area of the grain boundary. In small-angle grain boundaries, the main part of the grain boundary energy is the elastic energy of the grain boundary strain field, and the strain field is caused by the dislocation array that constitutes the grain boundary. Therefore, the grain boundary energy of the small-angle grain boundary and its relationship with the misorientation are expressed by equation (1.37). For large-angle grain boundaries, the core energy will be the main part of the grain boundary energy, and the change of the grain boundary energy with the misorientation angle θ is not obvious. The large-angle grain boundary energy of pure aluminum polycrystals containing 99.99% AI at room temperature is 0.6~1.1 J/m2.
Capacitors – Other defects in aluminum The above is an analysis of the grain boundary structure
3.Surface structure
The surface area of a crystalline solid generally includes a range of 1 to 1.5 nm extending inward and outward from the surface atomic termination plane as the reference. When a crystal has a surface, the three-dimensional periodic structure of atoms in the crystal will be damaged to a certain extent near the surface, and generally only involves a few atomic layers. This phenomenon of periodic structural destruction will cause the energy of the crystal system to increase. This additional energy is proportional to the surface area and is called surface energy, which will cause tension to shrink the surface. When the surface increases, external forces are required to overcome the surface tension and do work, so that the total energy of the surface increases. Surface energy is usually characterized by the work required to form a unit surface area, which is called specific surface energy (abbreviated as surface energy). It has the same dimension as the surface tension fs and is represented by ys (the unit is J/m2, or N/m), and fs=γs. Due to the anisotropy of crystals, the density and coordination number of atoms on different crystal planes are different, and the density of atomic bonds on different crystal planes is different. When external forces break these atomic bonds to make the relevant crystal planes become surfaces, the work required is different. Therefore, the surface energy of the crystal is closely related to the surface crystal type (hkl). The surface energy of aluminum is very sensitive to surface impurities, and it is difficult to accurately determine the intrinsic surface energy of aluminum crystals; generally speaking, its surface energy is higher than the grain boundary energy, and its estimated value is about 1 J/m2
. Under equilibrium conditions, the shape of the crystal should be surrounded by crystal planes with the minimum surface energy.
The surface of a crystal formed under normal non-equilibrium conditions generally deviates from the low surface energy surface to a certain extent. If the surface deviates slightly from the low index surface, it is called an adjacent surface, and if it is far away from the low index surface, it is called a rough surface. The adjacent surface will undergo a faceting process, that is, some atoms on the surface leave their equilibrium position and move to other positions to form new small planes close to the equilibrium state. This process ultimately reduces the total surface energy. Figure 1.42 (a) is a schematic diagram of unstable surface faceting. This surface contains terraces, steps and kinks, and Figure 1.42 (b) is a terrace-step-kink model of the surface. The terrace is a low-energy, close-packed low index surface, and the deviation of the surface from the low index surface is achieved by using steps and kinks that appear on the steps. There are also thermodynamically balanced point defects such as vacancies and additional atoms on the terrace surface; there are also positive and negative kinks on the steps with atomic scale; there will also be outcrops of defects such as dislocations and interfaces on the surface. As the temperature rises, terraces can also appear on the terraces, and each terrace has steps and kinks, making the surface a multi-layer terrace-step-kink surface.
When the actual crystal structure extends to the surface, the structure inside the crystal does not continue to the surface layer without change; in the direction perpendicular to the surface, the surface atoms lose their outer neighboring atoms and dangling bonds appear, so the surface layer and the atomic layer near the surface will relax and adjust their positions in a normal direction to reach a new equilibrium position and reduce the surface energy, which is called surface relaxation. Relaxation can continue for several layers of atoms on the surface, but from the outermost layer to the inner layer, the amount of deviation of each layer of atoms from the corresponding crystal plane spacing in the crystal decreases successively to appropriately reduce the surface energy. The unit cell distortion caused by surface relaxation is not very large.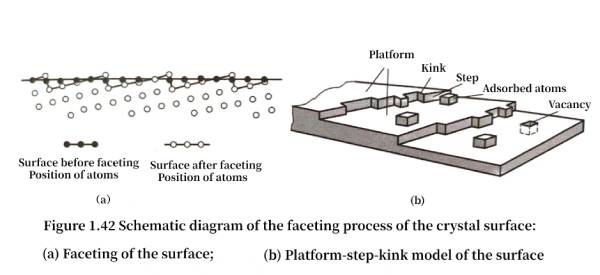
Capacitors – Other defects in aluminum The above is an analysis of the surface structure.
4.Capacitors – other defects in aluminum-Effect of surface oxide film on dislocation of aluminum foil
Dislocation near the boundary of two materials with different elastic moduli will also be affected by the image force. If the dislocation is on the side of the material with low elastic modulus, the interface will give repulsive force to the dislocation because the strain energy of it crossing the interface stress field is larger than the original one. In this way, when considering the effect of the aluminum surface on the dislocation, it is necessary to pay attention to whether the surface is covered by oxide. The elastic modulus of aluminum oxide is larger than that of aluminum. If the distance between the dislocation and the surface is relatively large, the effect of the oxide layer can be ignored; but when the distance between the dislocation and the surface is equivalent to the thickness of the oxide, due to the effect of the oxide layer, the force given to the dislocation by the surface may be repulsive.
Assume that there is a straight screw dislocation with a Burgers vector length of b and a dislocation line parallel to the surface in the aluminum foil crystal at a distance d from the surface, and the surface of the aluminum foil is covered with a layer of aluminum oxide with a thickness of t; outside the aluminum oxide is air. To simplify the analysis, the crystal and the covering are assumed to be elastic isotropic bodies, and the elastic modulus of air is 0. From this, we can deduce that the expression of the surface image shear stress T borne by a straight screw dislocation parallel to the surface along the slip plane perpendicular to the surface is: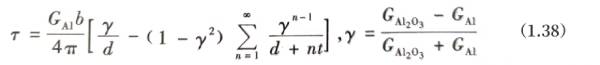
Formula (1.38) expresses the relationship between the distance d from the straight screw dislocation parallel to the surface to the aluminum foil surface, the thickness t of the oxide film on the aluminum foil surface, and the image shear stress T borne by the screw dislocation, which can be used to analyze the effect of the oxide film on the dislocation near the aluminum foil surface.
Figure 1.43 shows the corresponding relationship of the force on the straight screw dislocation near the pure aluminum surface covered with an oxide film calculated using formula (1.38); in the calculation, GAI=26GPa is taken for pure aluminum, GAI203=;175GPa is taken for aluminum oxide, the length of the pure aluminum Burgers vector is b=0.2863nm, the highest order number π of the sequence image dislocation in formula (1.38) is 10,000, and the oxide film thickness is taken as infinity, 200nm, 20nm, 6nm, 2nm and 0nm, i.e., the free surface. Figure 1.43 shows that for infinitely thick alumina, there is always an image shear stress T < 0, that is, no matter what the d value of the straight screw dislocation is, the surface will always repel the straight screw dislocation. When there is no alumina coverage, there is always an image shear stress T > 0, that is, no matter what the d value of the straight screw dislocation is, the surface will always attract the straight screw dislocation.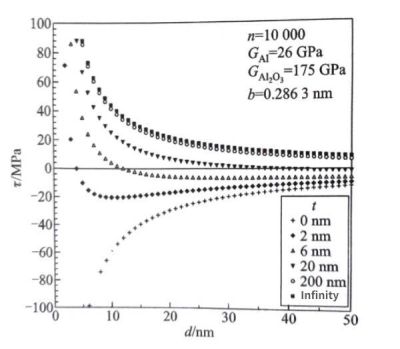
Capacitors – Other defects in aluminumFigure 1.43 Theoretical calculation of the shear stress of the straight screw dislocation image near the pure aluminum surface covered with aluminum oxide film
As the thickness of the aluminum oxide film decreases, the image stress decreases. The oxide film with a thickness of several nanometers to tens of nanometers is common on the surface of pure aluminum. At this time, the positive and negative signs of the image shear stress T will change at the appropriate position under the surface of the pure aluminum crystal (Figure 1.43). The screw dislocation at a high d value will be subjected to stress attracted to the surface, while at a low d value, it will be subjected to stress repelled from the surface. The critical shear stress Tc that causes pure aluminum dislocations to start is usually less than 1MPa. If the surface of the image shear stress T is the dislocation slip plane, it may cause the screw dislocation to slip and accumulate near the position where the image stress sign changes. As the thickness of the aluminum oxide film decreases, the dislocation accumulation will gradually approach the interface between pure aluminum and aluminum oxide; when the thickness of the aluminum oxide film decreases to a certain extent, it may break due to the stress field of the accumulated dislocation, and cause the accumulated dislocation to overflow the interface.
If the anodized aluminum foil is alkaline washed before the corrosion process, the oxide film on the surface of the aluminum foil can be removed to form a free surface. At this time, the dislocations on the surface of the aluminum foil will readjust their configuration under the action of the free surface imaging force, and some dislocations may even escape from the surface, reducing the surface dislocation density, which in turn affects the subsequent corrosion pore formation behavior.
Capacitors – Other defects in aluminum The above is an analysis of the influence of surface oxide film on dislocations in aluminum foil
Capacitors – Other defects in aluminum-Summary:
Capacitors – Other defects in aluminum This paper mainly analyzes the influence of vacancies, grain boundary structure, surface structure and surface oxide film on aluminum foil dislocation in detail. For more information about capacitor, please click https://xuansncapacitor.com/
